Continue to Site

Welcome to EDAboard.com

Welcome to our site! EDAboard.com is an international Electronics Discussion Forum focused on EDA software, circuits, schematics, books, theory, papers, asic, pld, 8051, DSP, Network, RF, Analog Design, PCB, Service Manuals... and a whole lot more! To participate you need to register. Registration is free. Click here to register now.

Register Log in

Is the loop stable in this case? and how to get a transfer function out of a wave?

Status
Not open for further replies.
A

aburdo

Newbie
Joined
Dec 20, 2021
Messages
5
Helped
0
Reputation
0
Reaction score
0
Trophy points
1
Activity points
52
Hi all,

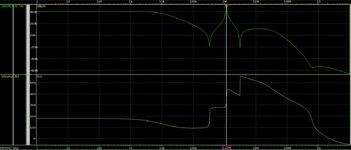
I am wondering how to know if a loop is stable in the case attached. (Loop gain is attached).
As I understand, if I get to a phase of 0 (or 360) with a gain of greater than 1, then the loop won't be stable.
So if I am correct, the example should be unstable, but I just can't make it oscillate.
1. I tried to make the loop oscillate by putting a voltage pulse with different amplitudes and different widths on the loop itself.
2. I tried to push(pull) a current pulse to(from) a high impedance node with different amplitudes and widths.

Nothing makes it oscillate.

Another note: I also want to make a model from this, so I need to get a transfer function out of this PWL.
Any idea how to do so? I tried to use matlab's identification tools box. I am able to get a "model output" (button in the GUI of the tool) with a fit of 99.9%, but if I look at the "frequency response" button, the graph I get is completely different and exporting the transfer function also fit the "frequency response" and not the "model output".
Any idea of what am I doing wrong?
Or any other suggestion of how to get a transfer function out of the graph below?

Thanks a lot everyone
 

Attachments

  • LSTB example.JPG
    LSTB example.JPG
    139.3 KB · Views: 132

Sort by date Sort by votes
My understanding to make an oscillator is you need unity gain as opposed to gain of >1. A gain of 1 will maintain the signal whereas a amplified gain will enentually hit the upper limits or saturate or blow up.
 

Upvote 0 Downvote
I think you should analyse such a circuit or system on the complex plane, on a so called Nyquist diagram or Nyquist plot.
I think because your curve doesn't encircle the -1 point of the real axis on Nyquist plot, it won't oscillate and it represents a stable system.

en.wikipedia.org

Nyquist stability criterion - Wikipedia

en.wikipedia.org en.wikipedia.org
 

Upvote 0 Downvote
Last edited:

Upvote 0 Downvote
scopeprobe said:
My understanding to make an oscillator is you need unity gain as opposed to gain of >1. A gain of 1 will maintain the signal whereas a amplified gain will enentually hit the upper limits or saturate or blow up.
Click to expand...
Yes, that's true, with exactly 1 it should oscillate and with gain > 1 it should increase the amplitude of the oscillation or just hit the rail.
But in this case for some reason, the circuit is still stable and converge to the value it should have if it was stable.
--- Updated ---

danadakk said:
The Bode plot is adequate to predict instability -


With qualifier -

www.researchgate.net

can BODE PLOT be used to explain the system stability...

Bode plot of system can be used to explain its stability instead of pole zero plot? Bode plot can be used in paper for stability analysis?
www.researchgate.net www.researchgate.net



Regards, Dana.
Click to expand...
Of course Bode plot is sufficient for understanding the stability of a system.
According to the Bode plot I attached, I expected the system to be unstable, but I couldn't make the system unstable using a transient simulation.
--- Updated ---

frankrose said:
I think you should analyse such a circuit or system on the complex plane, on a so called Nyquist diagram or Nyquist plot.
I think because your curve doesn't encircle the -1 point of the real axis on Nyquist plot, it won't oscillate and it represents a stable system.

en.wikipedia.org

Nyquist stability criterion - Wikipedia

en.wikipedia.org en.wikipedia.org
Click to expand...
I did try to look at it in the polar dimension .
The Nyquist diagram does encircle the -1 point...
 

Attachments

  • Nyquist plot.JPG
    Nyquist plot.JPG
    71.3 KB · Views: 102
Last edited:

Upvote 0 Downvote
aburdo said:
I did try to look at it in the polar dimension .
The Nyquist diagram does encircle the -1 point...
Click to expand...
Quote from wiki page: "Any clockwise encirclements of the critical point by the open-loop frequency response (when judged from low frequency to high frequency) would indicate that the feedback control system would be destabilizing if the loop were closed."

Your curve encircle -1, but counter-clockwise. Which can be necessary for closed-loop stability.
danadakk said:
The Bode plot is adequate to predict instability -
Click to expand...
Bode can be used to, it represents same data, but easier in above case to use Nyquist with such a chaotic transfer function. Bode is good for linear amplifiers, OPAmps mainly.
 

Upvote 0 Downvote
A circuit with feedback that fulfills Barkhausens oscillation condition will NOT necessarily oscillate because this condition is not a sufficient one. The system can go into saturation without any oscillation.

Recently, an additional condition has been found which must be fulfilled for oscillation:

The phase slope of the loop gain function at the frequency wo (loop gain equal or slightly larger than unity) must be negative (positive group delay): d(phi)/d(w)<0.
As we can see, this condition is not fulfilled for your sysytem.
 
  • Like
Reactions: aburdo

    G

    G4BCH

    Points: 2
    Helpful Answer Positive Rating
Upvote 0 Downvote
frankrose said:
Quote from wiki page: "Any clockwise encirclements of the critical point by the open-loop frequency response (when judged from low frequency to high frequency) would indicate that the feedback control system would be destabilizing if the loop were closed."

Your curve encircle -1, but counter-clockwise. Which can be necessary for closed-loop stability.

Bode can be used to, it represents same data, but easier in above case to use Nyquist with such a chaotic transfer function. Bode is good for linear amplifiers, OPAmps mainly.
Click to expand...
OK, I see that it does circle the -1 point clockwise...
This might explain why it seems to be stable in transient.
 

Upvote 0 Downvote
LvW said:
A circuit with feedback that fulfills Barkhausens oscillation condition will NOT necessarily oscillate because this condition is not a sufficient one. The system can go into saturation without any oscillation.

Recently, an additional condition has been found which must be fulfilled for oscillation:

The phase slope of the loop gain function at the frequency wo (loop gain equal or slightly larger than unity) must be negative (positive group delay): d(phi)/d(w)<0.
As we can see, this condition is not fulfilled for your sysytem.
Click to expand...
The system works like if it is a stable one. It doesn't oscillate and it doesn't saturate to anyplace except for the correct closed loop solution.

You mentioned an additional criterion for stability. I haven't encountered this condition anywhere. Could you reference me to the article or the source you've took it from?

Thanks
 

Upvote 0 Downvote
frankrose said:
Counter-clockwise...
Click to expand...
I am probably doing something wrong.
I am drawing the Nyquist plot by plotting "-lstb()" and "conjugate(-lstb())".
So I see that "-lstb()" is counter-clockwise to the "-1" point.
The "conjugate(-lstb())" is clockwise to the "-1" point.

I assume that I should look at the conjugate as the continuation of the lstb line, so it is like saying I have 2 counter-clockwise circles of "-1"?
 

Upvote 0 Downvote
I am not sure, but I think conjugate of your method represents the transfer function for the negative frequencies, which you can consider it encircles the -1 point clockwise, but with positive frequencies the function should do it counter-clockwise (for stable closed loop). I considered the yellow curve on your plot as response for the positive frequencies.
 
Upvote 0 Downvote
"You mentioned an additional criterion for stability. I haven't encountered this condition anywhere. Could you reference me to the article or the source you've took it from?"

See here (for example):
ieeexplore.ieee.org

Experimental investigation of the impact of phase vs. frequency characteristic properties on steady state oscillation existence in feedback oscillators

In this contribution we present the results of computer simulations as well as real experiments which all confirm the correctness of amendments to what is known as the Barkhausen criterion, necessary for its further application in practice [1]. The Barkhausen criterion for the formation of...
ieeexplore.ieee.org ieeexplore.ieee.org
and
ieeexplore.ieee.org

Barkhausen criterion and another necessary condition for steady state oscillations existence

Recent times have given rise to interesting discussions about the necessary and sufficient criteria for steady state oscillations of electronic circuits. The aim of this paper is to point out that the Barkhausen criterion (Bc), while a necessary condition for oscillations, but not a sufficient...
ieeexplore.ieee.org ieeexplore.ieee.org
 
Last edited:

Upvote 0 Downvote
  1. The magnitude of product of open loop gain of the amplifier and magnitude of feedback factor should be unity.
  2. Total phase shift around the loop should be zero ( 0 ).

Implied is system is linear, the additional constraint discussed is if
system becomes non linear, eg. goes into saturation, then there is
no guarantee it can oscillate because the Barkhausen criteria no longer
apply. Think of phase, for example, when a system is saturated what is
the phase shift ? Its now unknown .....Same for G, what is G when
system is saturated ?


Regards, Dana.
 

Upvote 0 Downvote
I wonder where you got this. The quoted formulation of Barkhausen criterion is at least massively mistakable. I guess "infinite gain" refers here to closed loop gain of an unstable feedback system. You should better refer to the clear original criterion in literature. loop gain T(s = jw0) = 1

Limitation of the criterion has been already addressed. Behavior of nonlinear systems is an even wider topic but shouldn't be mixed up with basic stability criteria of linear systems.

Control theory has methods to analyze behavior of non-linear systems. A simple intuitive way is to look at phase and magnitude of the fundamental wave.

You see e.g. that amplifiers with limited slew rate expose additional phase lag in large signal range. It once happened to me to design a cascaded integrator filter that started to oscillate after applying a large signal burst.
 
Last edited:

Upvote 0 Downvote
FvM said:
I wonder where you got this. The quoted formulation of Barkhausen criterion is at least massively mistakable. I guess "infinite gain" refers here to closed loop gain of an unstable feedback system. You should better refer to the clear original criterion in literature. loop gain T(s = jw0) = 1

Limitation of the criterion has been already addressed. Behavior of nonlinear systems is an even wider topic but shouldn't be mixed up with basic stability criteria of linear systems.

Control theory has methods to analyze behavior of non-linear systems. A simple intuitive way is to look at phase and magnitude of the fundamental wave.

You see e.g. that amplifiers with limited slew rate expose additional phase lag in large signal range. It once happened to me to design a cascaded integrator filter that started to oscillate after applying a large signal burst.
Click to expand...
I also picked up on the infinite and edited the post earlier.

Here is interesting paper on the topic -

www.researchgate.net

(PDF) The Barkhausen Criterion (Observation?)

PDF | A discussion of the Barkhausen Criterion which is a necessary but NOT sufficient criterion for steady state oscillations of an electronic circuit.... | Find, read and cite all the research you need on ResearchGate
www.researchgate.net www.researchgate.net

For many years we have seen that some basic circuit theory textbooks introduce the Barkhausen Criterion as the necessary and sufficient criterion for an electronic circuit to be an oscillator. Also the concept of linear steady state oscillators is introduced. The aim of this discussion is to point out that steady state oscillators must be non-linear circuits and linear oscillators are mathematical fictions.
Click to expand...

Regard, Dana.
 

Upvote 0 Downvote
I'd call LvW to comment the above statement. It sounds to me like throwing the baby out with the bath water. Stability criterion for linear systems has a purpose on its own. Stability of the original circuit in post #1 can be completely analyzed by linear theory.
 

Upvote 0 Downvote
Well - what should I say?
1.) The well-known Barkhausen criterion is a necessary condition only.
2.) It applies to a linear system and is used to design oscillator circuits providing sinusoidal signals.
3.) With respect to a safe start of oscillatons and due to parts tolerances the loop gain LG is slightly "over-designed" (|LG|>1 at zero phase). This situation is called "modified Barkhausen condition".
4) In order to arrive at a "good" sinusoidal signal, in addition, a certain non-linearity must be part of the circuit which brings the loop gain back to unity for rising amplitudes (most simple case: Supply voltage limitation).
5.) As a consequence (and due to time delays in the feedback circuit), the loop gain will swing slightly below and above unity under steady state conditions. (The pole pair is swinging between two points to the left and right of the imag. axis of the s-plane).
6.) When a third condition (see my post #13) is added to the two Barkhausen conditions (unity loop gain with zero phase), this condition can be regarded as a sufficient criterion.
 

Upvote 0 Downvote
Thanks for the detailed explanation.

I presume, the aditional phase slope criterion is still not sufficient for cases with multiple encirclements of the (-1,0) point in Nyquist diagram?
 

Upvote 0 Downvote
FvM said:
Thanks for the detailed explanation.

I presume, the aditional phase slope criterion is still not sufficient for cases with multiple encirclements of the (-1,0) point in Nyquist diagram?
Click to expand...
Yes - I think, you are right (probably?). I should think about it - although nobody who wants to build an oscillator would design such as ystem.
 

Upvote 0 Downvote
Status
Not open for further replies.

Similar threads

Part and Inventory Search

Welcome to EDABoard.com

Sponsor

Back
Top