tarun0xe
Member level 2
hello everyone...the file i have attached,contains a problem based on kirchoff's current law in which one needs to find all mentioned currents.i have proceeded by combining node A and B into one(since they are same potential points so they must be same node,i guess) and similarly combining node C and D too.in this way,i have applied KCL at node E say,which is the combination of nodes A and B and found currents i1,i4 and i10but what about current i2 and i3?????? they are not even present in my equivalent circuit....
in solution,after finding above currents i1,i4 and i10 KCL is again applied individually at nodes A and B in given figure to find i2 and i3....well thats simple but i thought that current i2 and i3 shouldn't exist as they are shown between same potential points A-B and C-D respectively and i think no current exists between same potential points......so where am i lagging the concepts..????please give your usefull suggestions....thanks in advance..:smile:...
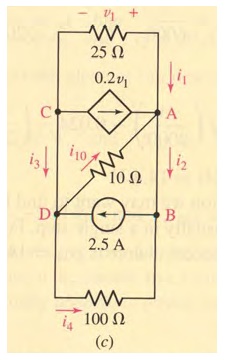
in solution,after finding above currents i1,i4 and i10 KCL is again applied individually at nodes A and B in given figure to find i2 and i3....well thats simple but i thought that current i2 and i3 shouldn't exist as they are shown between same potential points A-B and C-D respectively and i think no current exists between same potential points......so where am i lagging the concepts..????please give your usefull suggestions....thanks in advance..:smile:...
