north2012
Member level 3

Hi,
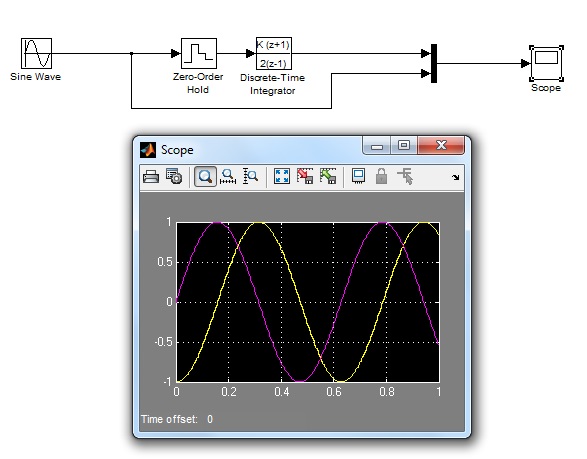
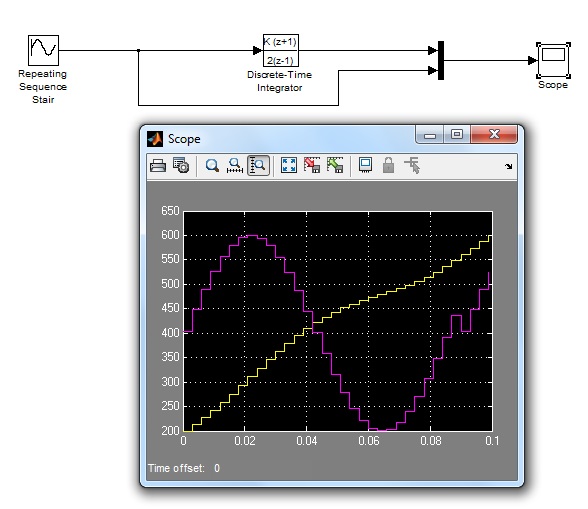
I would like to implement integration of input signal to my AVR based system. Input signal will be sampled with ADC and output will be sent to DAC. For example, if input signal is x(t)=Xsinwt => ADC => x[k] => integration => y[k => DAC => y(t)=-Ycoswt
Ideas?
I would like to implement integration of input signal to my AVR based system. Input signal will be sampled with ADC and output will be sent to DAC. For example, if input signal is x(t)=Xsinwt => ADC => x[k] => integration => y[k => DAC => y(t)=-Ycoswt
Ideas?