Bardia_Sahami
Newbie level 2

Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.





ASCII art can be improved by using code tags.I have had to use dots instead of spaces.

Hi everyone,
Is there anyone knows how to to calculate the Req of this circuit? n tends to infinite.
View attachment 158900
Thanks in advance.
PS - the numbers you see are based on ohm. like the resistor with "3" means a 3 ohm-resistor. (Numbers are the resistance value based on ohm)
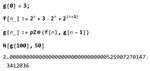

I don't know if there is a closed form solution to your problem, because each resistor segment you add to the right of your network is a different ohmage value. However, with a computer, one can easily iteratively add a a large finite number of increasing resistor value segments and observe where the total resistive value of the network is heading. The computer program below does exactly that. It adds 100 resistor segments to the 3 ohm resistor on the left and computes the final value to 50 decimal places. It doesn't take many brain cells to see that the convergence is at 2.0 . Add the leftmost 1 ohm and 2 ohm resistors and one gets the final network resistance of 5 ohms for an infinite sequence. I will leave it to someone else to figure out a closed form solution. Ratch
View attachment 159006



I don't understand the syntax, but I think something is wrong with the program.
I get the total resistance to 2.25 + sqrt(2.25^2 + 2*2.25) = 5.3423292....
Since this probably is a school assignment, I will not reveal the method now.

Is there anyone knows how to to calculate the Req of this circuit? n tends to infinite.

First steps:
1. Consider the first step of the ladder: ignore the rest: it is 1+3+2=6
2. Consider the next step of the ladder: ignore the previous and the following steps: you get 2+6+4=12=6x2
3. The n-th step of the ladder will be, by induction: 6x2^(n-1)
4. All the steps are in parallel connection: so you need to add the reciprocals:
((1/6)*(1/1 + 1/2 + 1/4 + ... to infinity)
5. The sum to infinity is not tough to calculate. It will be 2.
The equivalent resistance will be 1/((1/6)*2)=1/(1/3)=3.

This is not correct. All "steps" are not in parallel.

There is a simpler way:
Take the sum as S
Note that if you remove the first step of the ladder, you are left with a ladder whose value is 2S
So we get S=1+3||(2*S) +2=3+3*2*S/(3+2*S)
Solve this equation to get S; one root will be negative and ignore that.

this is basically the same method that I used for post #7