twig27
Newbie level 6
Hello,
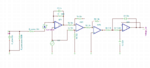
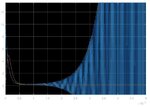
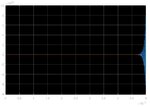
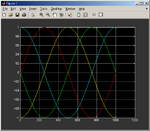
I have the transfer function of a system in the s-domain. For a given output I want to obtain the input. The most natural way to me seems to multiply the output with the inverse of the
transfer function. The problem in implementing this e.g. in Matlab is, that the inverse transfer function would have more zeros than poles which leads to an error.
Another idea is for example to implement a block diagram in simulink. The input is my output signal and in the negative feedback I put the original transfer function. This approach, however does not lead to the desired results.
I'm glad for any hints!
I have the transfer function of a system in the s-domain. For a given output I want to obtain the input. The most natural way to me seems to multiply the output with the inverse of the
transfer function. The problem in implementing this e.g. in Matlab is, that the inverse transfer function would have more zeros than poles which leads to an error.
Another idea is for example to implement a block diagram in simulink. The input is my output signal and in the negative feedback I put the original transfer function. This approach, however does not lead to the desired results.
I'm glad for any hints!