SanjKrish
Member level 3

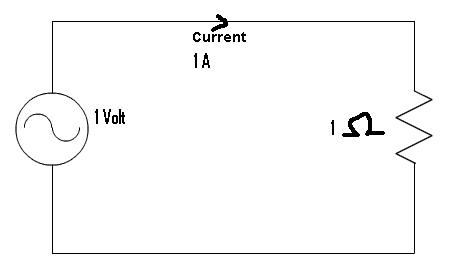
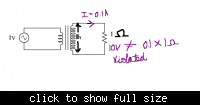
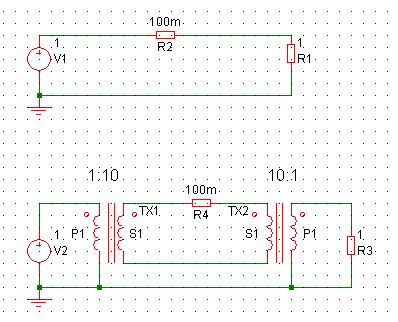
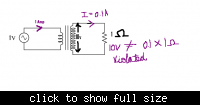
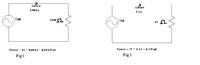
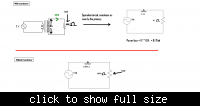
I read that a step up transformer increases the voltage decreasing the current..
But by ohms law when voltage is high the current flowing through it should also be high
The two statements are contradicting.. Can anyone help me understand this..
If I were to compare it with water analogy.. more pressure should cause more water to flow in the pipes... but what a transformer does is, it increases the pressure but decreases the water flow...
Plz help me understand..
But by ohms law when voltage is high the current flowing through it should also be high
The two statements are contradicting.. Can anyone help me understand this..
If I were to compare it with water analogy.. more pressure should cause more water to flow in the pipes... but what a transformer does is, it increases the pressure but decreases the water flow...
Plz help me understand..
Last edited: